Лекция 2

Выделяют главное значение аргумента - это такое значение, которое лежит на полуинтервале $(-\pi ,\pi ]$. Обозначение: $\arg z$.

Комплексное число $z=x+iy$ можно записать в виде $z=x+iy=r\cos \phi +ir\sin \phi =r(\cos \phi +i\sin \phi )$ ($+$ можно рассматривать как символ, объединяющий мнимую и вещественную часть, а можно как символ сложения).

Запись комплексного числа в виде $z=r(\cos \phi +i\sin \phi )$, $r>0$ - модуль комплексного числа $z$, а $\phi$ - одно из значений аргумента $z$, называется тригонометрической формой записи комплексного числа.

• Равенство чисел ⇐> равенство модуля и (аргумента + $2\pi k$).

• Умножение двух чисел, записанных в тригонометрической форме - модули умножаются, аргументы складываются (легко проверить).

• Деление двух чисел, записанных в тригонометрической форме - модули делятся, второй аргумент вычитается из первого (легко проверить).

• Возведение в степень - формула Муавра (по индукции - база)

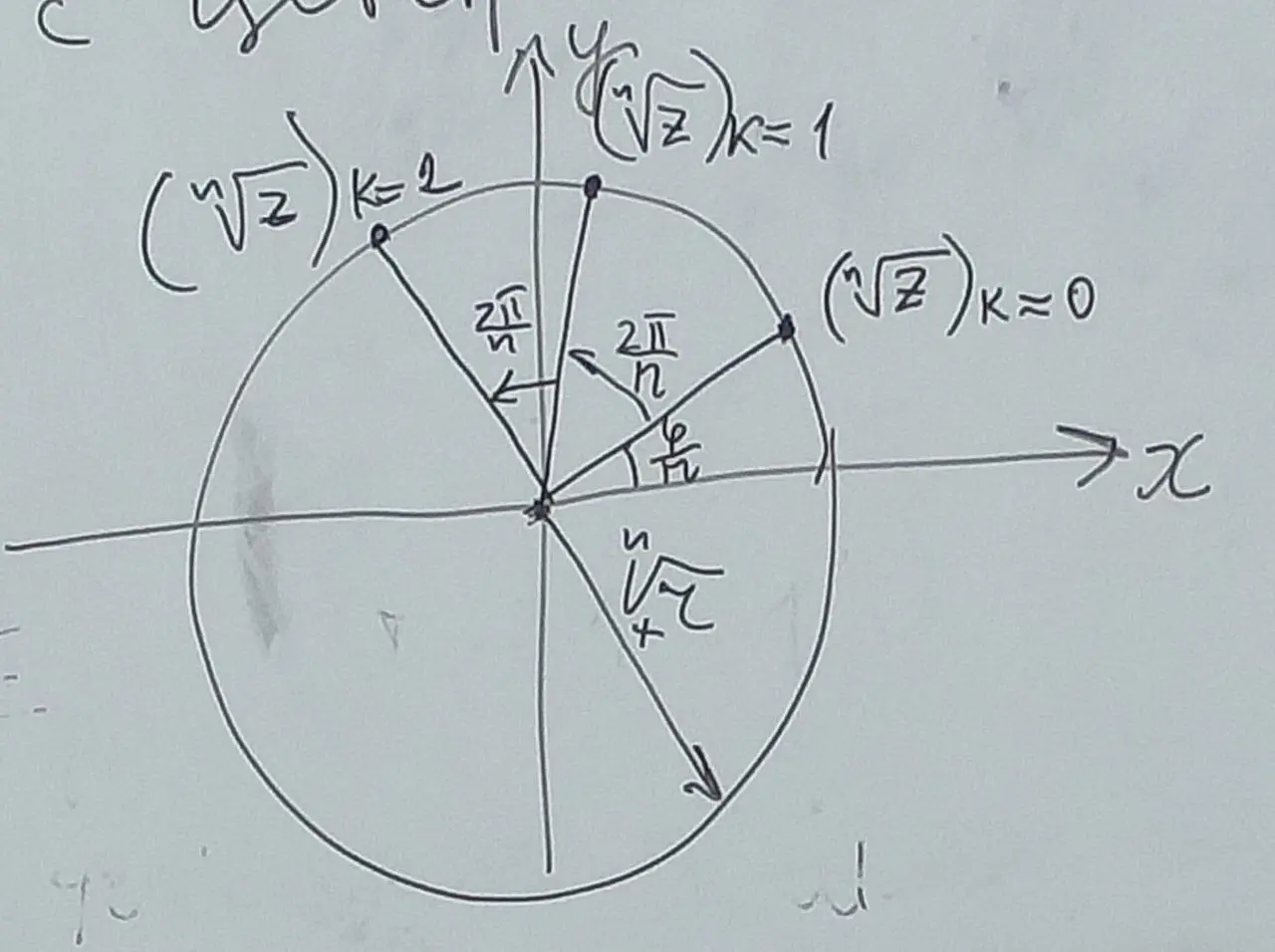
Число $w$ называется корнем $n-$й степени ($n\ge 2$, $n\in \mathbb{N}$) из числа $z$, если $w^n=z$. Обозначение: $w^n\sqrt{z}$. Последний символ означает совокупность (ин-во) всех корней $n-$й степени из $z$.

Если $z=0$, то и $w=0$ - в этом случае имеется лишь одно значений корня. Пусть $z\ne 0$, запишем его в тригонометрической форме $z=r(\cos \phi +i\sin \phi )$. Если $w^n=z$, то ясно, что $w\ne 0$. Поэтому можно написать $w=\rho (\cos \theta +i\sin \theta )$. После возведения в степень получаем равенство $w^n={\rho }^n(\cos n\theta +i\sin n\theta )=r(\cos \phi +i\sin \phi ))$. Последнее равенство справедливо тогда и только тогда, когда ${\rho }^n=r$ и $\theta =\frac{\phi +2\pi k}{n}$, $k=0,\pm 1,\pm 2,\dots$.

Последние соотношения означают, что $\rho {=}^n\sqrt{r}$ (в смысле школьной алгебры), $\theta =\frac{\phi +2k\pi }{n}$. Поэтому ${}^n\sqrt{z}{=}^n\sqrt{r}(\cos \frac{\phi +2k\pi }{n}+i\sin \frac{\phi +2k\pi }{n})$.Два корня равны тогда и только тогда, когда целым кратным $2\pi$ является разность их аргументов: $\frac{\phi +2k_1\pi }{n}-\frac{\phi +2k_2\pi }{n}=\frac{k_1-k_2}{n}\cdot 2\pi$, то есть тогда и только тогда, когда $k_1\equiv k_2(\mathrm{mod}n)$. Таким образом, значения корня равны ⇐> $(k_1\equiv k_2)(\mathrm{mod}n)$.

Поскольку числа $0,1,\dots ,n-1$ попарно не сравнимы по модулю $n$, то для получения всех значений корня $n$-й степени из $z=r(\cos \phi +i\sin \phi )$ следует в выражении ${}^n\sqrt{r}\left(\cos \frac{\phi +2\pi k}{n}+i\sin \frac{\phi +2k\pi }{n}\right)$ положить $k=0,1,2,\dots ,n-1$. Таким образом, для $z\ne 0$ имеется в точности $n$ различных значений корня $n$-й степени из этого числа. Все эти значения располагаются в вершинах правильного $n$-угольника, вписанного в окружность радиуса ${}^n\sqrt{|z|}$ с центром в начале координат.

Пусть дана последовательность комплексного числа $\{z_n\}$ комплексных чисел $z_n=x^n+i{y}^n$. Ясно, что такая последовательность однозначно определяется двумя последовательностями вещественных чисел. Ясно, что число $A+ib$ является пределом этой последовательности, если $\exists$ число $N$ такое, что если $n\ge N$, то $|z_n-A|<\epsilon$.

Для доказательства следующей теоремы нам потребуется такое двойное неравенство. Пусть $z_1=x_1+i{y}_1$, $z_2=x_2+i{y}_2$, тогда