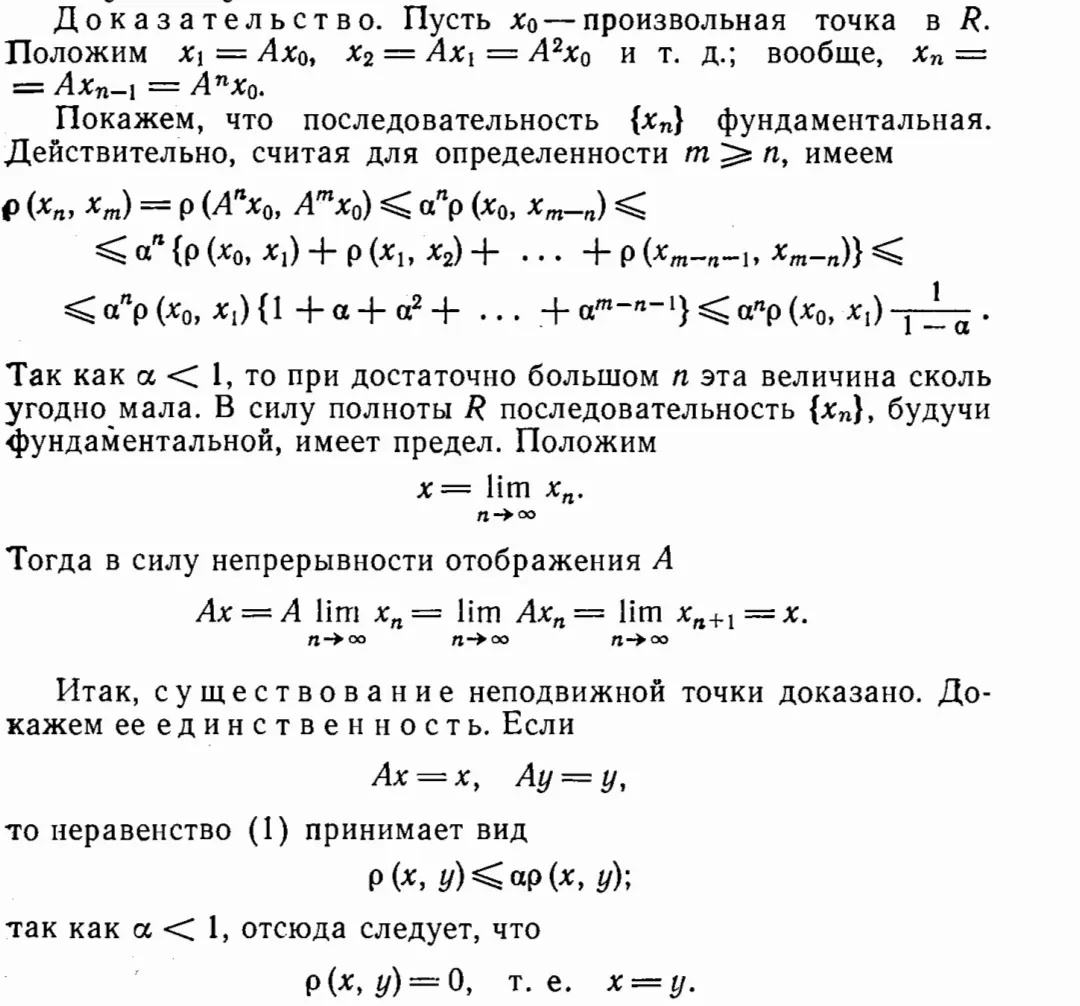Теорема о вложенных шарах
Метрическое пространство полно тогда и только тогда, когда каждая последовательность вложенных шаров, радиусы которых стремятся к нулю, имеет общую точку
Доказательство
Необходимость полно и пусть - последовательность вложенных друг в друга замкнутых шаров. Пусть - радиус, а - центр шара .
Пусть пространство
Последовательность центров фундаментальна, поскольку и при .
Положим , тогда . - точка прикосновения для каждого шара . Но так как - замкнутое множество, то для всех (замкнутое множество содержит все свои точки прикосновения).
Достаточность
Теорема Бэра
Полное метрическое пространство не может быть представлено в виде объединения счетного числа нигде не плотных множеств
Доказательство , где каждое из множеств нигде не плотно.
Предположим противное. Пусть
Пусть - некоторый замкнутый шар радиуса . Поскольку множество не плотно нигде, то оно не плотно и в . Тогда существует замкнутый шар радиуса меньше , такой, что и .
Поскольку множество не плотно в , по той же причине в шаре содержится замкнутый шар радиуса меньше , для которого .
Мы получаем последовательность вложенных друг в друга замкнутых шаров , радиусы которых стремятся к нулю, причем . Мы получаем последовательность вложенных друг в друга замкнутых шаров , радиусы которых стремятся к нулю, причем .
В силу теоремы о вложенных шарах пересечение содержит некоторую точку . Эта точка по построению не принадлежит ни одному из множеств , следовательно, , то есть , в противоречии с предположением.
Теорема о неподвижной точке
Всякое сжимающее отображение, определенное в полном метрическом пространстве , имеет одну и только одну неподвижную точку
Доказательство