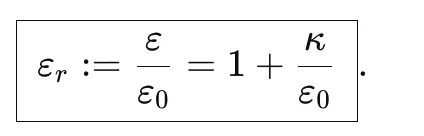Вопрос 16

Электрический дипольный момент $\overrightarrow{p_e}$. Поляризованность вещества. Электрическое поле внутри диэлектрика. Диэлектрическая проницаемость $\epsilon$. Связь между нормальной составляющей вектора $\vec{P}$ и поверхностной плотностью связанных зарядов.

---

Электрический дипольный момент

Простейшей системой точечных зарядов называется электрический диполь. Так называется совокупность равных по величине, но противоположных по знаку двух точечных зарядов $-q$ и $+q$, сдвинутых относительно друга на некоторое расстояние.

Электрический момент диполя

Пусть $\overline{l}$ - радиус-вектор, проведенный от отрицательного заряда к положительному. Вектор $\overline{p}=q\overline{l}$ называется электрическим моментом диполя или дипольным моментом.

Дипольный момент системы: $\vec{p}={\sum }_i{q}_i\overrightarrow{r_i}$

Поляризованность вещества

Допустим, что диэлектрик состоит из электрически нейтральных молекул. Под действием приложенного электрического поля центр тяжести электронов в молекуле немного смещается относительно центра тяжести атомных ядер. Молекулы становятся электрическими диполями, ориентированными положительно заряженными концами в направлении электрического поля $\vec{E}$. В этом случае говорят, что диэлектрик поляризован, а само смещение положительных и отрицательных зарядов диэлектрика в разные стороны называют электрической поляризацией. 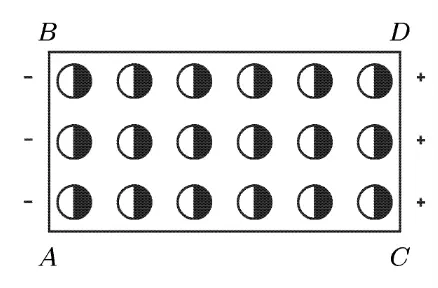Для количественного описания поляризации диэлектрика пользуются вектором поляризации. Так называется дипольный момент единицы объёма диэлектрика, возникающий при его поляризации: $\vec{P}={\lim }_{\Delta V\to \infty }\frac{1}{\Delta V}{\sum }_{\Delta V}{\vec{p}}_k$

Связь между нормальной составляющей и поверхностной плотностью

Пример

Возьмем кусок однородного изотропного диэлектрика, имеющий форму косого параллелепипеда.

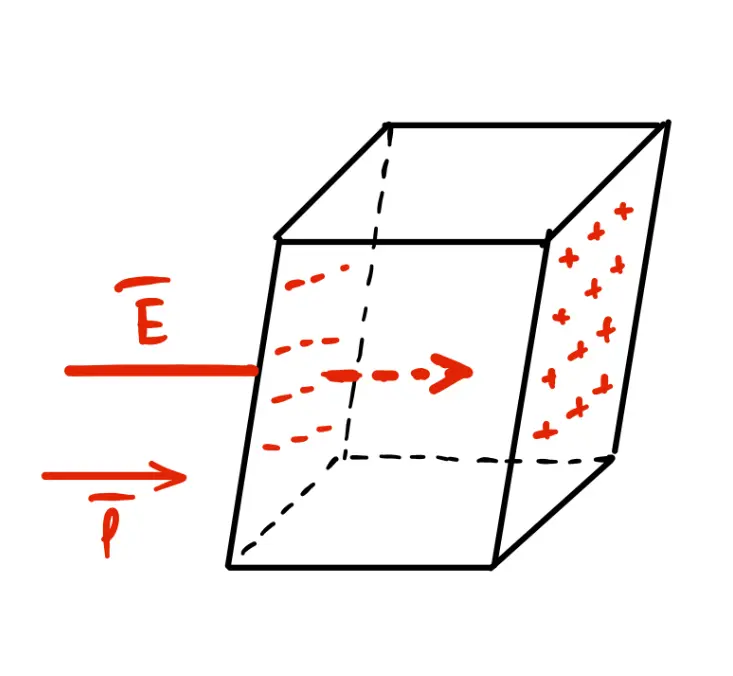
Поместим его в однородное электрическое поле, направленное параллельно боковым ребрам. На основаниях параллелепипда появятся поляризационные заряды с поверхностной плотностью ${\sigma }_{пол}$. На боковых гранях поляризационных зарядов не возникнет, так как смещение зарядов внутри диэлектрика происходит параллельно этим граням.

Если $S$ - площадь основания параллелепипеда, то диэлектрик приобретет дипольный момент ${\sigma }_{пол}S\vec{l}$, где $\vec{l}$ - вектор, проведенный от отрицательного основания параллелепипеда к положительному параллельно боковым ребрам. Вектор поляризации диэлектрика будет $\vec{P}=\frac{{\sigma }_{пол}S}{V}\vec{l}$ Пусть $\vec{n}$ - единичный вектор внешней нормали к основанию параллелепипеда, заряженному положительно. Тогда $V=S(\vec{l}\cdot \vec{n})$ (площадь основаня на высоту). Подставив в формулу вектора поляризации, получим ${\sigma }_{пол}=\vec{P}\cdot \vec{n}$

Хз надо или нет

Введём вектор электрической индукции $\vec{D}={\epsilon }_0\vec{E}+\vec{P}$ Дифференциальная форма теоремы Гаусса для диэлектриков имеет вид $\rho =\text{-div}D,$ где $\rho$ - объёмная плотность свободных зарядов. ? Далее, исходя из свойств дивергенции, $\rho =-{\epsilon }_0\text{div}\vec{E}+\text{div}\vec{P}$ $\text{div}\vec{E}=-\frac{\rho -\text{div}\vec{P}}{{\epsilon }_0}$ С другой стороны, как следствие из общей теоремы Гаусса, $\text{div}\vec{E}=\frac{\rho +{\rho }_{пол}}{{\epsilon }_0}$ В итоге получаем $-\text{div}\vec{P}={\rho }_{пол}$

Диэлектрическая проницаемость

В изотропных диэлектриках поляризация пропорциональна полю $\vec{P}=\kappa \vec{E}$

Подставляя в определение $\vec{D}$: $\vec{D}$ = $({\epsilon }_0+\kappa )\vec{E}\equiv \epsilon \vec{E}$

Безразмерная проницаемость